The idea of the electromagnetic spectrum is one of those great scientific syntheses of observable natural phenomena that should be part of the knowledge of any scientifically educated person. Other similar syntheses are things like the kinetic-molecular theory of matter, the concept of the vastness of the Universe and our relation to it, the idea of deep time and the evolutionary development of life, the DNA code of life and the ideas of basic biochemistry.
Since the information technologist makes use of the electromagnetic spectrum a great deal, it is appropriate to devote a lecture to it in our course.
These were two disparate ideas that were first discovered in antiquity: the Greeks gave the name (as in so many areas) through their term for amber. Amber is a naturally occurring fossizilized tree sap, made famous in the movie Jurassic Park. Anyway, the Greeks had observed that amber when rubbed could attract small pieces of dust or other light trash. Also, static electricity sparks were also known.
Naturally occurring magnetic material ("lodestone" or a type of iron oxide with a higher concentration of iron than usual) was also known to the ancients. It is said that the Chinese were aware that a piece of lodestone could be floated on a piece of cork, and would stabilize to a consistent North-South orientation, thus making possible a compass.
Hewever, it wasn't until the 1700s that the beginnings of our modern "scientific" approach to electricity and magnetism began.
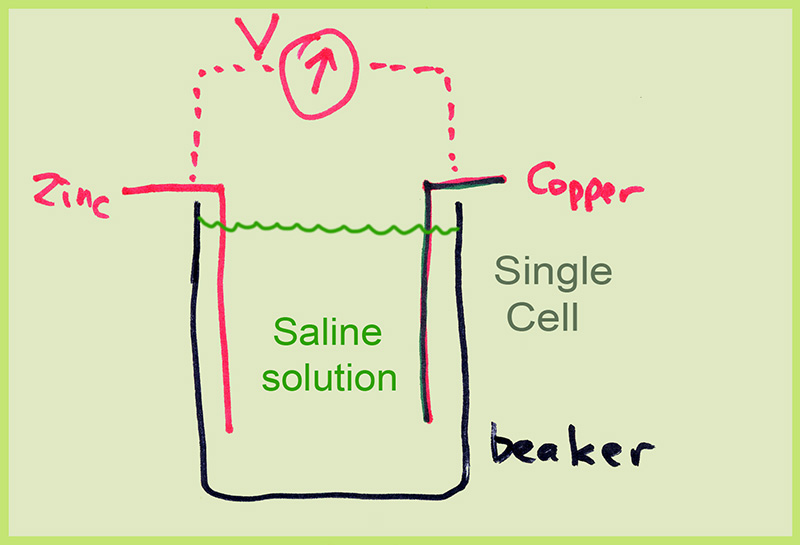
Alessandro Volta noted a connection between electricity and life when he made dissected frogs legs twitch by touching them with dissimilar metals. [This inspired Mary Shelley, the wife of the famed poet Percy Byssche Shelley, to write a famous novel, whose theme was "There are things that Man is not meant to know..."] Anyway, Volta had been experimenting with placing dissimilar metals, e.g. copper and zinc, into salt solutions, and obtaining an electric current.

A single cell produces about 1 volt of potential. By daisy chaining cells, he could obtain hundreds of volts. His device is now the electrochemical "cell" or "battery" (strictly speaking, a battery is more than one cell, usually connected in daisy chain ("series") to give a higher voltage, as in the square 9 volt "batteries".
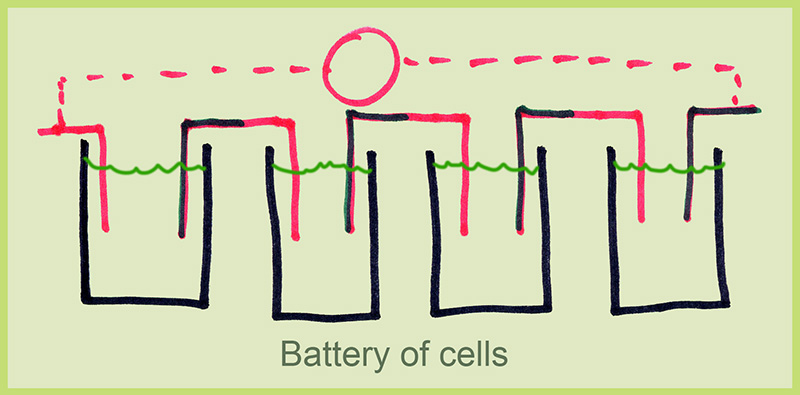
Single cells give 0.5-2 volts, batteries higher, e.g. 9v batteries). Cells such as those shown are rather useless in practice due to the fact that the chemical reaction products diffuse rapidly across the cell and neutralize the activity. Modern cells use a dense mat of material to reduce this diffusion.
It was early shown that if wire was wrapped into a coil, and connected to a battery, that a magnet was produced in the area close to the coil. If a piece of iron was placed inside the coil, the field was greatly magnified, giving a device called an electromagnet. If the iron was a hard steel alloy, it would retain the magnetism after the current was removed, allowing the manufacture of permanent magnets. Lodestones were quite weak compared to artificial magnets.
Hans Christian Oersted observed that if a wire was wrapped around a compass, the compass would deflect.
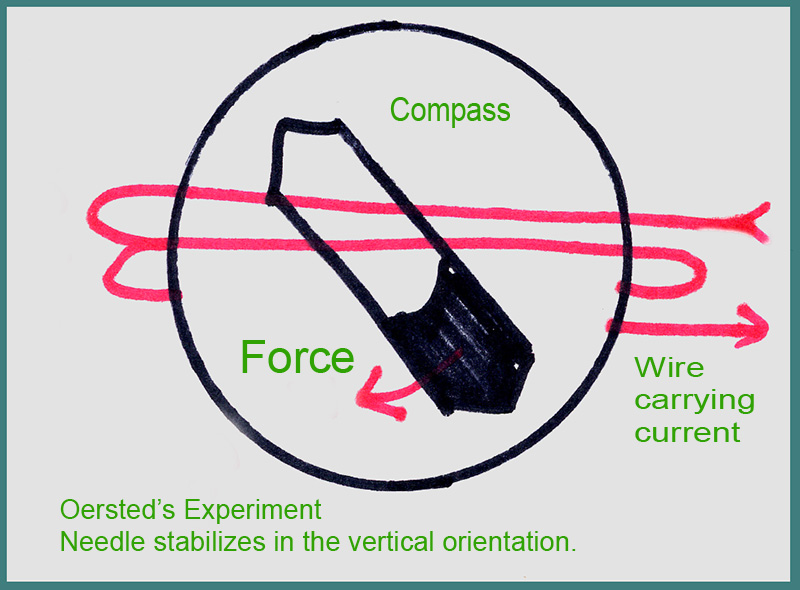
This was a unique phenomenon. The uniqueness came from the fact that the interaction was at right angles. The compass needle didn't line itself up with the wire, but at right angles to it. This was the first "vector cross product" relationship discovered. All other interactions hitherto known acted in a straight line between centers: gravitational attraction, electric force and magnetism.
Scientists had been experimenting with pure electric force also. To observe pure electric force out in the open requires charges of thousands of volts, which, fortunately, are easily obtained by friction. When you give someone a shock by "static electricity" you are using thousands of volts. It is not lethal because the amount of electric current is small.
[I use the term "scientists" here. In those days, in the 18th and 19th centuries, the usual term was "philosophers" or "natural philosophers". Our "science" was their "natural philosophy."]
[One can make water analogies of these ideas; in fact any electrical device can have a water analogy. One can think of electric charge as being a quantity of water, current as the rate of flow of water, and voltage as the force or pressure propelling the water. The force or pressure comes from a source of energy; either the water must be pumped up to a height to give it pressure-that is, the water has potential energy, or else a pump must take energy from some other source to force the water to move directly. Our city water system uses a combination of both methods. Strictly speaking, voltage is called potential difference, and represents the potential energy per unit charge, measured between two points in space.]
So, simple experiments can be done with light objects like pith balls, showing the force between them, such as shown in schematic form below:
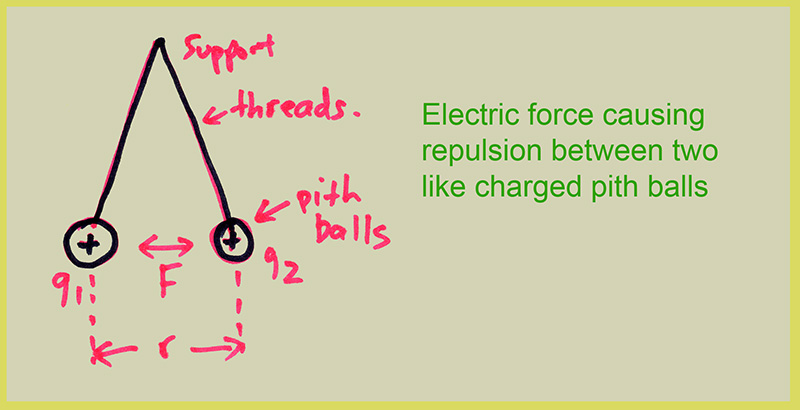
Study of this sort of thing led to the relation between electric force and distance as
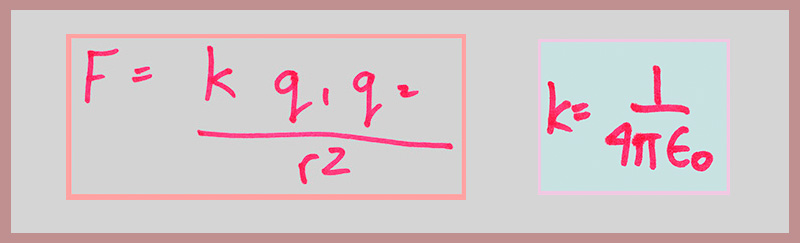
The formula shows that the force between two static charged objects q1 and q2 varied as the amount of charge and inversely as the square of the distance between them, the "inverse square law" which had been shown by Kepler and Newton to apply also to gravity in the Solar system.
Modern physicists use the 1/4pi epsilon zero formulation for the constant in our rationalized system of units.
These studies were being carried out mainly in Europe, especially France and Italy. England was mainly preoccupied with the developing industrial revolution, and its scientific workers were clarifying ideas about energy and thermodynamics, motivated by the development of the steam engine.
America was regarded by European intellectuals as a land of wild Indians and stagecoaches, if they thought about it at all. The idea that someone in America could do Natural Philosophy seemed absurd. However, Benjamin Franklin in the middle of the 1700s had a brief period in his life when he had made enough money from his printing shop to semi retire, but hadn't become embroiled in the American Revolution as representative in France yet.
He experimented with electricity, leading up to his famous kite experiment in which he showed that lightning was the same basic thing as static electricity created in the lab. Since he knew that lab static dissipated quickly if the charged object had sharp points on it, he thought that maybe lightning could be dissipated before the actual stroke if sharp objects electrically connected to the earth were to be placed on high roofs. This was shown to be effective. Some feel that this vivid demonstration of the ability of man to evidently interfere with the "will of God" successfully was a significant force leading to the growth of secularism in Christendom. There was, after all, no more vivid demonstration of the "will of God" than to be struck down by a lightning bolt!
A similar formula was shown to work for idealized magnetic poles:
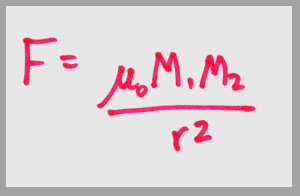
The constant mu zero is used to make the numbers work out. M1 and M2 are the magnetic pole strengths. [In fact this equation is an idealization more so than the electric equation above. An isolated magnetic pole is an unachievable abstraction-in practice magnets always exist as dipoles-N and S poles fairly close together. Electric poles can in principle be separated as much as needed.]
By the middle 1800s quite a bit of electrical technology had been worked out. Things like telegraph lines were beginning to appear, allowing instant communication over vast distances. In fact, the mid 19th century saw communication finally surpass that under the Roman Empire 2000 years earlier!
Electric batteries, motors, generators existed. Electric power stations were starting to appear.
James Clerk Maxwell studied all the disparate physics and engineering involved in this field, and formulated a theoretical formulation that tied it all togther. This led to the great triumph of "field theory" in which each point in space could be thought of as posessing a magnetic and electric force; that is, there existed an electric and a magnetic field. Oersted had shown that these were related, and the electric motor and generator were the practical embodiment of this discovery.
Mathematically, Maxwell produced what every red-blooded theorist would die for-a compact set of equations that unite a vast and apparently disparate set of phenomena into a single structure. His equations are shown below:
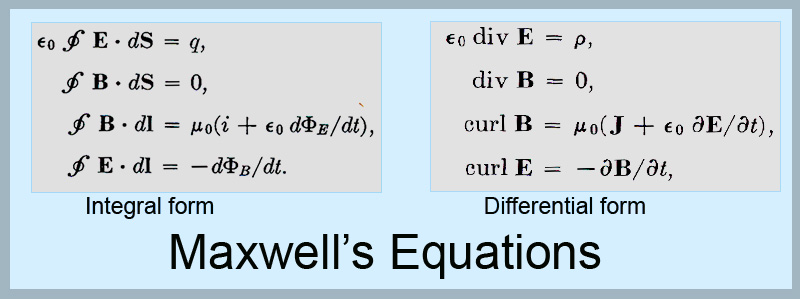
Physics students learn about these when they study electromagnetism in 2nd or 3rd year. A good part of the early technical education of a would-be physicist is to learn the necessary mathematical tools, that is, integral and differential calculus, to enable manipulation of these equations. A physicist has to learn how to apply these to specific real-world situations (albeit a bit idealized for pencil and paper calculations). This theory was a revolution in the 1870s when it appeared; it took a generation for it to be absorbed into the technical consciousness of physicists.
When undergraduate physics students first start to work with these equations, there is an understandable "rush" in their minds; all these amazing things revealed by such a small number of symbols. To me, an interesting issue is, Where does the information actually lie? After all, it takes an educational process spanning many years to enable the physicist to work with these equations; is the information in the symbols, or are the symbols a bit like very high level function calls in an API environment, in which they trigger a complex series of mental events that yield the result. The function call without its substrate of lower level operations would be useless. Maxwell's equations without the technical education are just so many hieroglyphics, as they may well seem to CPSC students!
A corollary of Maxwell's theory was the following equation:
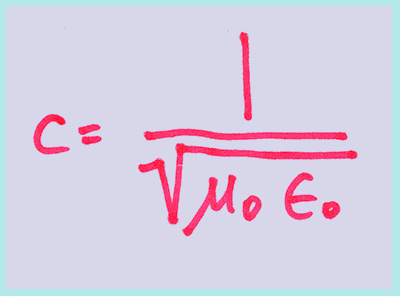
Maxwell initially formulated his theory based on an idea of the electromagnetic effect being due to a sort of fluid flow. From the basic equations, he worked out the speed of the interaction; this is a calculation including the two basic physical constants: the electric constant and the magnetic constant. Quantitatively, the velocity comes out to 3 E8 m/s, or the speed of light.
This immediately led to the idea that some sort of "electromagnetic" waves could exist, and the possibility that light might be such a wave.
Attempts to detect such waves were carried out by Heinrich Hertz, who demonstrated the first apparatus for creating and detecting low frequency electromagnetic waves, i.e. "radio". Since this page is already too long, I don't think I will discuss their simple receiver and transmitter (maybe say something in class).
In 1902, Guglielmo Marconi demonstrated the transmission of radio waves across the Atlantic. This was the beginning of the radio industry. One of the main applications was the implementation of ship to shore telegraph. Previously, a ship was completely out of touch with the world while on its voyage. The sinking of the Titanic in 1912 was an early example of the use of this technology to summon help.
Gradually, engineers learned how better to control radio waves, allowing for "wave bands" or fixed frequency "bands" allowing simultaneous use of electromagnetic waves by different people in the same area for different transmissions. Today, of course, we have this with our radio stations; we "tune them in" by adjusting our receiver to the desired band.
[As a side issue, what about the idea of a fluid for electromagnetism? This idea persisted for some decades, and was finally put to rest by the Michelson-Morley experiment, showing that no physical medium existed (or if it did, it carefully moved so as to nullify any attempt to measure the movement of any apparatus through it!) This led to Einstein's Special Theory of Relativity, and the equivalence of mass and energy, and the atomic bomb.]
A diagram of the electromagnetic spectrum is shown below:
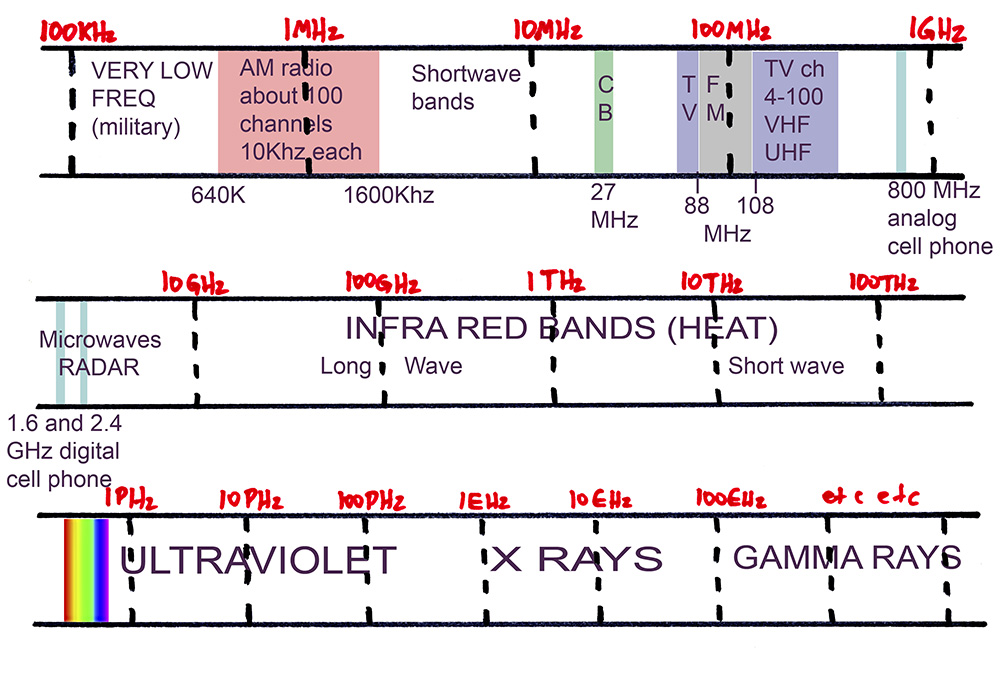
Let's look at it a bit at a time.
In principle there is no lowest frequency. Astrophysicists have detected frequencies as low as about 10E-7 Hz, or about one cycle per year caused by motions of cosmic objects, and there is no reason not to think that frequencies go many orders of magnitude lower. [An order of magnitude is a factor of 10, that is, 300 is about an order of magnitude larger than 30. The term "order of magnitude" is normally used to give very approximate comparisons.]
Since the speed of electromagnetic waves is 3X10E8 m/s in vacuum (very slightly slower in air), the wavelength at 100KHz would be
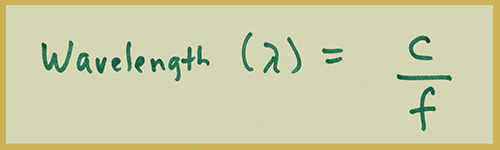
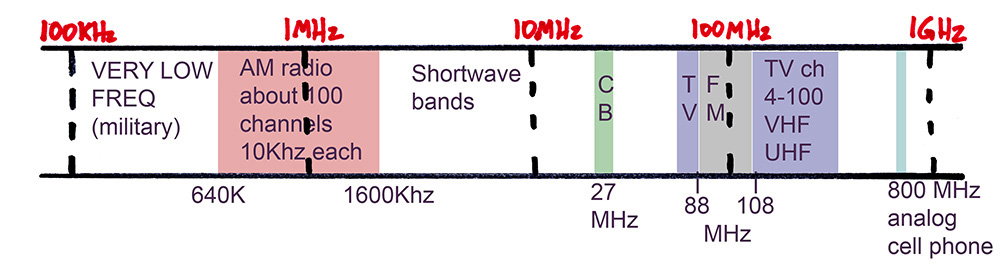
3x10E8 / 100 x 10E3 = 3000 meters, approx, or 3 km. Such a long wave can "diffract" around obstacles, such as the earth itself, and thus can be picked up worldwide. These Very Low Frequency (VLF) bands have been used by the military.
Early radio technology was of necessity very simple minded, one might say crude. Although high frequencies could carry more information (see Shannon's Law below) the simple electronic valves (i.e. "tubes") could only operate at relatively low frequencies, in the megahertz region. Thus, the first broadcast channels appeared around 1 MHz.
A channel can be thought of as an independent path for information. Modulation is the process of coding information into a channel. A technique called "amplitude modulation" or AM allowed audio information to be coded into a radio frequency channel of narrow bandwidth, in fact only double the frequency range of the audio itself. Since audio goes to 20KHz, this would imply that an AM channel of 40 KHz width would be needed. In fact, it was decided to use a bandwidth of only 10 KHz, since this was adequate for the sound reproduction technology back in the 1920s when radio appeared. [Radio killed off much live theater, vaudeville, and the domestic sale of pianos!] Thus, we had about 100 possible channels in the range 600-1600KHz.
A problem with all electromagnetic channels is that in any one reception area, only one channel at any one frequency is usable. Because AM radio stations "carry" quite a long way-the lower frequency ones diffract around the earth's curvature, the higher frequency ones bounce off the ionosphere, especially at night, the 100 channels must be spread around the country fairly thinly. If two channels on the same band are picked up at the same time by a receiver, a squealing noise is heard.
Above the AM band, a number of miscellaneous AM bands developed for various services, collectively called "short wave". The ionospheric bounce was particularly effective in some of these bands, making them useful for military transmissions, and propaganda broadcasts, especially in the "Cold War" from 1950 to 1990. I can remember as a teenager playing with shortwave tuning into Russian rantings (in English) about the "dictatorship of the Proletariat". I can't imagine who would want to listen to this!.
Relatively recently, a band at about 27MHz was allocated for AM Citizen's Band radio. This originally had 24 channels, later expanded to 40. You can see how narrow the CB band looks on the diagram, compared to AM radio. This is due to the logarithmic plot I have used for frequency in the horizontal axis. More modern technology has allowed these higher frequencies, where there is more room for channels, to be used economically, with the aid of "crystal filters" and "frequency synthesis" techniques, not available in the 1920s.
An inventor named E H Armstrong invented many of the basic analog circuits used for radio receivers. A problem with AM radio was its lack of noise rejection. He conceived of the use of another technique, frequency modulation or FM. This would need about 10 times the bandwidth per channel, requring the use of higher frequency bands where there would be enough Hz available. He worked with RCA, who gave him the use of a laboratory and a transmitter setup on the roof of one of the new New York skyscrapers then being built. However, as mentioned in a previous page, Sarnoff, the head of RCA, decided to throw his resources into the development of television. Thus, FM lost the support of RCA, Armstrong committed suicide, and TV ended up with much of the spectrum space. You can see FM squeezed in between the TV channels. RCA threw Armstrong a bone by making the TV audio frequency modulated, but the picture is AM.
Each FM band gets 100KHz, which Armstrong felt was a sell-out; he wanted more. Each TV band takes about 4500Khz, with channels about 6000Khz apart. This separation allowed cheap TV receivers to reliably receive adjacent channels in the same market area.
The long carry of short wave stops working at around 20MHz, so that TV and FM stations are basically "line of sight." This necessitates high transmitting antennas, and allows each major market to have lots of available channels.
In effect, a copy of the electromagnetic spectrum can be carried inside a cable, as an electrical analog, up to frequencies of about 500MHz or so. So, we have cable TV and other services, compatible with the airborne electromagnetic channels.
Finally, at 800 MHz, we find the original cell phone band, used for analog phones.
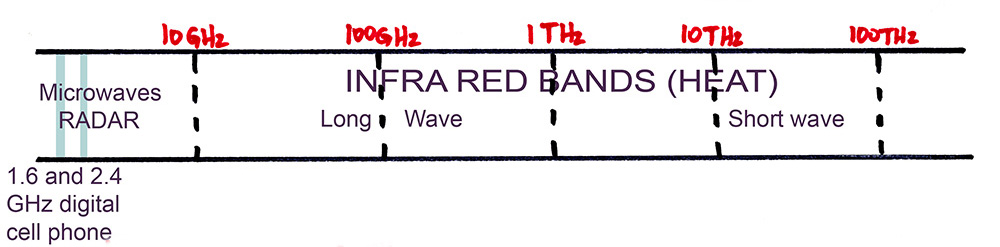
The next image shows the two digital cell phone bands. I need to find out what bands WI-FI uses, and the upcoming ultra high speed wireless network bands. This latter, I understand, uses "spread spectrum" technology; the information is carried using many different frequencies rather than on single frequencies. This makes interference a serious problem, except that the power is kept very low, reducing range.
Historically, the TV and Cell bands were originally used only for RADAR (Radio Direction and Ranging). This was developed as a crash program during World War 2. Like many technologies, it was invented by the British but developed elsewhere, in this case the USA. The British invented the "cavity magnetron" vacuum tube, in which high voltage electrons are injected into a very strong magnetic field, causing them to swirl in a curved path, oscillating at the desired gigahertz frequencies. [When this was first demonstrated to the Americans, one of the leading scientists, I I Rabi, said "It's easy-an analog of a whistle" prompting one of the others there to remark sourly "OK, Rabi, how does a whistle work?"] In fact many audio devices and microwave devices are analogous, since the wavelengths are similar. Treble frequencies for audio have mechanical waves similar in length to gigahertz electromagnetic microwaves.
Radar was very crude in its use of the frequencies, basically just an on-off setup. Our modern cell phones are far more sophisticated in their modulation techniques, allowing thousands of channels in any local area.
Apart from crude things like microwave ovens and heat lamps, a huge stretch of the electromagnetic spectrum is currently unused. One reason is that our atmosphere is opaque to these frequencies. This in fact is a cause of the greenhouse effect. The short wave infrared can penetrate the atmosphere, coming from the Sun. It is absorbed by the earth, and re-emitted as long wave infrared. This is because the earth is much cooler than the Sun, and the wavelength produced by an emitter of electromagnetic radiation shortens as its temperature rises.
We generate radio by electrical excitation. Heat will alwo generate it, although not in a useful fashion, as there is a mess of random frequencies produced. Frequencies like our TV would be characteristic of temperatures very close to absolute zero.

Finally, we reach the visible band, a very narrow strip from about 400 to 800 THz. This band exists because our atmosphere is transparent in this narrow range, and our eyes thus work in this area. Fortunately, the air blocks ultraviolet except the very near UV. This is fortunate because this is the start of the bands that can disrupt chemical bonds.
We are starting to make use of light in CPSC, for fiber optics. Certainly, there are a lot of Hz there. However, our modulation is still rather crude, although it is improving; in fact, unexpected improvements may have contributed to the great internet "bust" in 2001. Companies laid huge amounts of long distance fiber, expecting that each fiber could carry maybe 5 channels. So, methods of sending 200 channels appear, resulting in a vast oversupply of fiber bandwidth! Channels can be sent over fiber using different colors. This is called "wave division multiplexing". I suppose our AM and TV channels could rejoice in the same term!
Visible light in many ways is a "watershed" in terms of wavelength and frequency. The visible band shows both particle and wave characteristics, depending on what experiment is done to observe. Visible light shows wave effects like diffraction and interference, but also shows particle like effects (e.g. the photoelectric effect; Einstein got his Nobel from his explanation of this effect, not from relativity).
A whole treatise could be written on the physical causes of visible colors. Basically, they result from energy transitions within atoms, of electrons moving from one state to another. Colors toward violet are caused by higher energy transitions. As we move into the UV, the transitions can involve molecular disruption. The Ozone Layer blocks near UV; if it gets through the degree of molecular disruption on the surfaces of living things becomes an issue, with skin cancer, etc, possibly becoming a serious problem.
Continuing to higher frequencies, X rays are characteristic of very high energy electron transitions. They are produced in CRTs by the electrons slamming with 20000 Volt potential into the inner face of the tube. The tubes are made with lead glass to block these X rays. "Harder" X-rays come from low level nuclear disruption; the nucleus of the atom is about 6 orders of magnitude smaller than the atom itself, and about 6-7 orders of magnitude harder to change in state. Nuclear changes of state (e.g. atomic or hydrogen bombs, or the core of the sun) release gamma rays.
There are isolated extremely high energy gamma rays, about 10 orders of magnitude beyond my diagram, occasionally seen. Their source has been a mystery for decades; I believe some tentative explanations now exist.
The Bell Telephone System ran the telephone network in much of the USA until the late 1970s or early 1980s as a government regulated monopoly-almost a public utility. Since they had a protected position, with a guaranteed profit, they could engage in long term research into issues related to communications.
Since by law they could not sell ancillary discoveries for profit, they basically gave away many of their great developments, such as the transistor. [We might note that their Unix developed just as the Bell system was being broken up by the US Government, and the legal restrictions were also being removed. So, Bell started trying to sell Unix licenses, for an amount about equal to the gross national product of Luxembourg, with the predictable result that several non Unix Unices developed, thus "forking" the development of the system, producing several incompatible versions, and thus aiding Microsoft in its march to hegemony.]
1948 was a great year. The transistor was announced to the world, the Manchester University (England) "Baby" electronic computer ran the first stored program in June, and Claude Shannon announced his communication theory. (Also, I was born, two days before the run of the "Baby" and about 150 miles away).
Shannon worked much of his professional life at Bell Labs. His main claim to fame is his study into the error-free information capacity of an analog channel. (We mustn't forget as we think about digital technology that it all is really analog underneath). Analog operation involves continuous functions of variables such as voltage, current, time.

Earlier, Harry Nyquist, also of Bell Labs, had studied some of these issues; his most famous product being the Nyquist Sampling Theorem, which states that the highest frequency present in an analog input, such as sound, must be sampled at least twice in a cycle to guarantee error-free reproduction.

Shannon studied the encoding of information in a channel, and formulated his equation relating the possible bit rate. He showed that the bit rate of a channel depends on the analog bandwidth in Hertz, and the signal to noise ratio.
Noise is any unwanted energy; it arises from many causes. The most basic is thermal noise caused by the random motion of atoms and molecules in all matter. Noise comes in from the cosmos also; some of the "snow" visible on a TV with an antenna if tuned to a vacant channel may be from this source [Some of this may be echoes of the Big Bang!]. Not surprisingly, human technology produces lots of noise; any electrical switching or sparking produces electromagnetic noise. Computers are of course changing state billions of times per second; each state change is physically done by voltages within the system changing. This will propagate electromagnetic noise. [In fact, there are regulations regarding the amount of RFI (Radio Frequency Interference, or noise) that can be produced by any electronic device. One problem with all this sort of regulation is that compliance is expensive; a small company must send its device to a consultant lab which will run the necessary tests and sign the forms that go to the regulators, a process that may cost $10,000 to $100,000. This process is especially onerous in Europe; where some have cynically suggested that one reason for the stiff regulations is that the big industries, like Siemens and Philips, can maintain staffs for dealing with compliance issues, while small companies face a serious barrier to entry in the marketplace as a result. In North America, the regulations are not so stiff, and in Asia, it is still the "Wild West" in many places.]
Signal to noise ratio is the ratio of the signal value (voltage, current, energy, pressure, or whatever) divided by that of the noise. I will use a value of 1000 in the examples below. This corresponds roughly to AM radio, or the telephone on a good day. High fidelity audio amplifiers can achieve values of around 100,000, limited by thermal noise in the transistors and resistors. [Professionals often measure this in decibels. For voltage or current measurements, the decibel (dB) value can be determined by multiplying the log (10) of the S/N by 20, so a S/N of 1000 would be 20x3 or about 60dB, and 100,000 would be about 100dB.]
Shannon's formula is shown below:
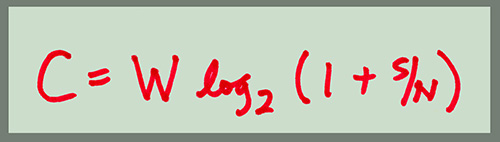
So, if we consider an AM radio channel, we can obtain an error-free data rate of
w = 10KHz for an AM channel
S/N = 1000 approx so log(2) of 1+1000 is near enough to 10
So, the data rate can be up to 10K x 10 = 100K bits/sec.
Moving up to television bands, we can calculate the data capacity of a TV channel (assuming 6MHZ bandwidth for the channel, and 1000 for S/N) to be about 6M x 10 = 60 Mbit/sec. A commercial regular DVD movie holds about 10 GB of data max. If this is devoted entirely to a movie, and lasts 2 hours, the data rate when you play the movie is 10GB/7200sec x 8bits/byte = 11.1 Mbit/sec. This gives an insight into how digital TV can share the old TV channels with legacy broadcasting. [The US is trying to legislate an end to analog legacy broadcasting, but each administration postpones this comfortably into the time of a different administration. If legacy broadcasting ended, we could either transmit higher resolution movies in the existing channels, or else split the channels to allow more of them. Which do you think is more likely to happen?]
Finally, let's consider light. The visible spectrum is about 4 x 10^14 Hz wide. If we use the same 1000 S/N we get a gross data capacity of 4 x 10^15 bits/sec, or about 4 x 10^14 bytes/sec, or about 4 x 10^8 Megabytes per second, or about 4 x 10^5 gigabytes per second, or about 4 x 10^4 DVD movies per second!
Unfortunately, this assumes that we can control light the way we can control radio frequencies, with detailed control over each electromagetic "vibration". This is not possible with light due to things like "Doppler broadening" caused by the thermal motion of the atome producting the light. However, much progress can be made from our current technology. [The data rate figure calculated above is a bit like the ideal single electron trap which could represent a memory cell. Our current DRAM technology requires about 100,000 electrons per bit. This suggests a fantastic possible improvement in RAM density! Quantum mechanics, in particular the Heisenberg Uncertainty Principle, seem to militate against the practicality of small single electron traps.]
(Q)Explain the physical basis of the force equations which define the quantities mu zero and epsilon zero.
(Q)Give a general account of Maxwell's ideas (you need not quote the actual equations) and explain how his theory suggested the notion of electromagnetic waves.
(Q)Give a brief historical summary of some of the basic discoveries that led to the concept of the electromagnetic spectrum.
(Q)Sketch the electromagnetic spectrum itself, showing the relative positions of the main bands. BONUS for quantitative details.
(Q)Explain the point of Shannon's Law, and give an example of a data rate calculation.